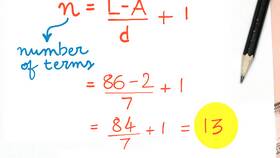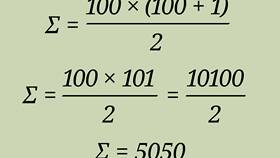Арифметическая прогрессия - это числовая последовательность, в которой каждый следующий член отличается от предыдущего на постоянную величину (разность прогрессии). Рассмотрим методы вычисления суммы членов такой прогрессии.
Содержание
Основные понятия арифметической прогрессии
| Первый член | a₁ - начальное значение прогрессии |
| Разность прогрессии | d - постоянное число, добавляемое к каждому члену |
| n-й член | aₙ = a₁ + d(n-1) |
Формулы для вычисления суммы
Через первый и последний член
Sₙ = n(a₁ + aₙ)/2
Где:
- Sₙ - сумма n первых членов
- n - количество членов
- a₁ - первый член
- aₙ - n-й член
Через первый член и разность
Sₙ = [2a₁ + d(n-1)]n/2
Пошаговый алгоритм вычисления
- Определите первый член прогрессии (a₁)
- Найдите разность прогрессии (d)
- Определите количество членов (n)
- Вычислите последний член (aₙ = a₁ + d(n-1))
- Подставьте значения в формулу суммы
Пример расчета
| Дано | a₁ = 3, d = 2, n = 5 |
| Последовательность | 3, 5, 7, 9, 11 |
| Вычисление | S₅ = 5(3 + 11)/2 = 35 |
Проверка правильности вычислений
- Сложите члены прогрессии вручную
- Используйте альтернативную формулу
- Примените математическое программное обеспечение
Особые случаи
| Бесконечная прогрессия | Сумма расходится при d ≠ 0 |
| Нулевая разность | Sₙ = n·a₁ (все члены равны) |
| Отрицательная разность | Формулы работают аналогично |
Применение в программировании
Пример на Python
- Через формулу:
def sum_arith_prog(a1, d, n):
return (2*a1 + d*(n-1))*n/2 - Через цикл:
sum_result = 0
current = a1
for _ in range(n):
sum_result += current
current += d
Историческая справка
Формула суммы арифметической прогрессии была известна еще в Древней Греции. Согласно легенде, учитель предложил ученикам сложить числа от 1 до 100, и юный Гаусс быстро нашел решение, заметив закономерность.
Понимание принципов вычисления суммы арифметической прогрессии важно для решения широкого круга математических задач и находит применение в физике, экономике и компьютерных науках.