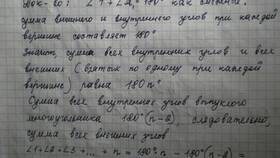Сумма внутренних углов выпуклого многоугольника - это важная геометрическая характеристика, которая зависит от количества сторон фигуры. Рассмотрим этот вопрос подробно.
Содержание
Основная формула
Для любого выпуклого n-угольника сумма внутренних углов вычисляется по формуле:
S = (n - 2) × 180°
где n - количество сторон (углов) многоугольника.
Примеры расчетов
| Фигура | Количество сторон (n) | Сумма углов |
| Треугольник | 3 | (3-2)×180° = 180° |
| Четырехугольник | 4 | (4-2)×180° = 360° |
| Пятиугольник | 5 | (5-2)×180° = 540° |
| Шестиугольник | 6 | (6-2)×180° = 720° |
Доказательство формулы
Формула выводится следующим образом:
- Из любой вершины n-угольника проводим все возможные диагонали
- Диагонали разбивают многоугольник на (n - 2) треугольника
- Сумма углов каждого треугольника равна 180°
- Общая сумма углов многоугольника равна сумме углов всех полученных треугольников
Сумма внешних углов
Для любого выпуклого многоугольника сумма внешних углов (по одному при каждой вершине) всегда равна 360°, независимо от количества сторон.
Практическое применение
- В архитектуре при проектировании зданий
- В компьютерной графике при моделировании объектов
- В геодезии при расчетах земельных участков
- В задачах на построение геометрических фигур